In particle physics experiments at facilities like the Large Hadron Collider, high-energy collisions produce complex events with multiple particles that must be reconstructed from detector measurements. A crucial step in analyzing this data is event reconstruction: identifying the original, short-lived particles produced in a collision and tracing them back to their parent particles. This process is essential for making new discoveries and precisely measuring particle properties.
However, event reconstruction faces a significant hurdle: the combinatorial challenge. When collisions produce many detectable particles, determining which of these came from which original particle becomes a complex task. The number of possible assignments can grow exponentially with the number of detected particles, making it computationally intractable for traditional methods.
Traditional methods, such as the χ² method and Kinematic Likelihood Fitters, attempt to assign detected particles to their hypothesized parent particles based on kinematic constraints. While successful, these methods can suffer from biases by forcing combinations to match exact particle masses, potentially leading to inaccurate measurements. More modern machine learning approaches, like those using attention transformers such as SPA-Net, have shown improvements in reducing these biases and handling the combinatorial complexity. However, even these methods often focus on identifying groups of particles without explicitly reconstructing the full decay chain or predicting the properties of the intermediate particles.
A Case Study: Top Quark Pair Production
To illustrate the combinatorial challenge, consider the case of top quark pair production in the all-hadronic decay channel, a process we focused on in our publication. In this process, both top quarks decay hadronically: each top quark decays to a W boson and a bottom quark, and each W boson subsequently decays to two quarks. This results in six jets in the detector. For such an event, there are 720 possible ways to assign these jets to the original particles. Even after accounting for symmetries, this number is reduced to 90. As the number of jets increases, this combinatorial complexity rapidly escalates; for seven jets, the combinations jump to 630, and for eight jets, it becomes 2520. This exponential growth highlights why traditional methods struggle to test every possible combination, especially in the high-multiplicity environments of LHC collisions.
The Topograph Solution: Physics-Inspired Graph Neural Networks
Topographs are inspired by Feynman diagrams, which are visual representations of particle interactions. In a Feynman diagram, particles and their interactions form a network, or a graph. Topographs build upon this concept by representing the particle decay process as a graph where:
- Nodes represent particles, both the observed final-state particles (like jets) and the unobserved intermediate particles (like W bosons and top quarks).
- Edges represent the connections between these particles, indicating a parent-daughter relationship in a decay.
Unlike previous graph neural network (GNN) approaches that often create fully connected graphs (where every particle is potentially connected to every other particle), Topographs inject the intermediate particles directly into the graph as their own nodes. This allows the network to explicitly learn the properties of these intermediate particles. Furthermore, instead of connecting all objects to one another, Topographs connect observed particles to their potential mother particles. This significantly reduces the complexity of the graph. For example, for a top quark decay, a fully connected GNN would have a quadratic number of edges, while a Topograph has a linear number of edges with respect to the number of reconstructed objects. This linear scaling is a crucial advantage, making Topographs computationally much more efficient for complex events.
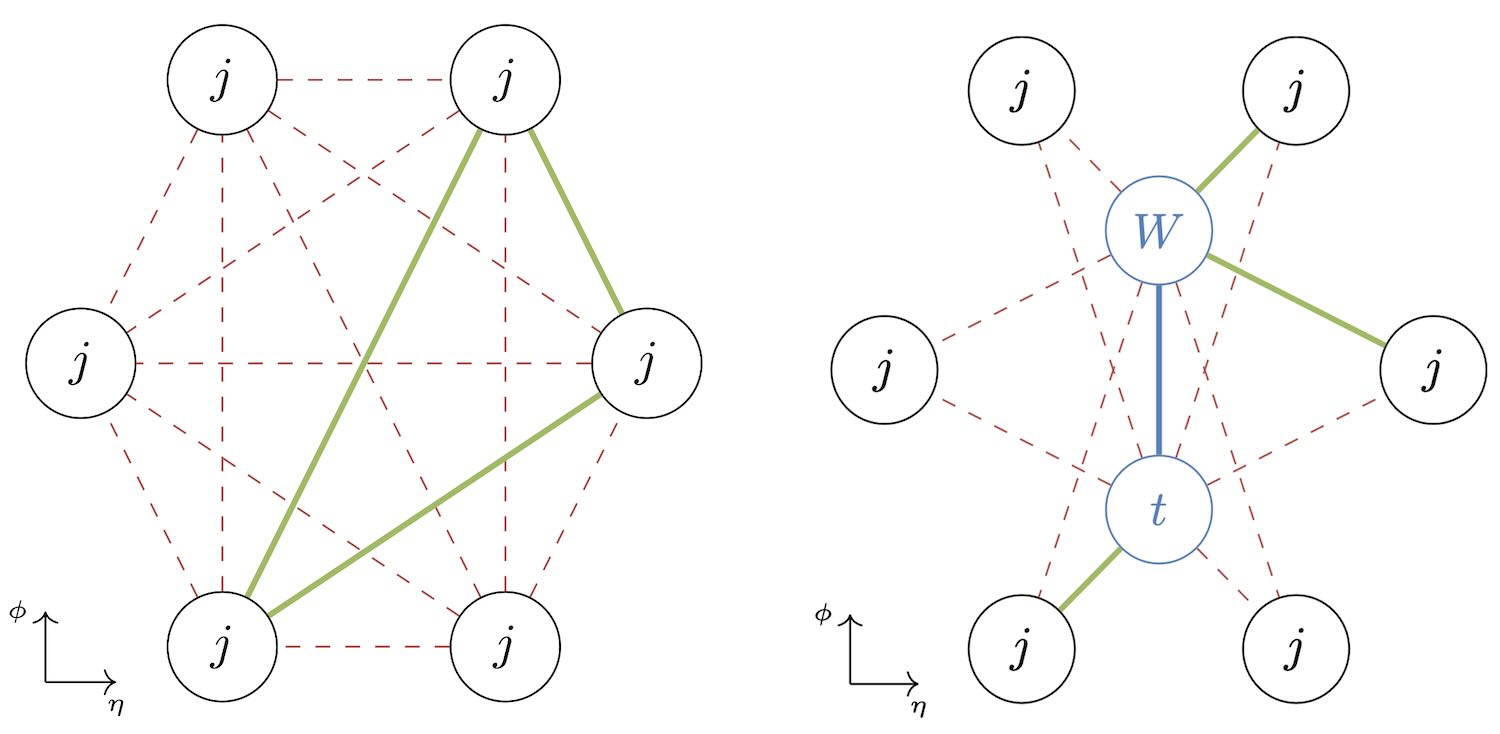Figure: Two solutions to the combinatorics problem: a fully connected graph (left) and a topograph (right). The topograph captures the decay structure while avoiding unnecessary connections. (Image: Phys. Rev. D 107 (2023) 116019)
How Topographs Work
The key innovation of Topographs lies in how they make predictions for the most likely jet assignment to the top quarks. The process works through several interconnected components:
-
Explicit Modeling of Intermediate Particles: Topographs inject nodes for intermediate particles—such as W bosons and top quarks—directly into the graph structure. These nodes are initialized using attention-weighted pooling from the input jets, where different networks generate attention weights for each intermediate particle type. This allows the network not only to assign jets to these particles but also to predict their kinematic properties through dedicated regression components.
-
Physics-Inspired Connections: The edges in the Topograph reflect known decay patterns, connecting daughter particles (jets) only to plausible parent particles. This physics prior constrains the graph in a meaningful way, reducing complexity and guiding the learning process toward physically valid solutions. For instance, jets are connected to both W boson nodes and top quark nodes – the connections follow the expected decay topology.
-
Message Passing for Information Exchange: Information flows along the graph through multiple message passing layers, enabling each node to update its understanding based on its connections. In our implementation, we use four message passing steps where jets, edges, and injected W and top nodes are iteratively updated. This iterative exchange helps the model refine both the particle assignments and the predictions of their properties.
-
Edge Scoring and Assignment: Every edge receives a learned score indicating how likely it is that the connected particles are related by a decay. These scores are calculated by passing the edge properties through a classification network. To resolve the combinatorics, we use an iterative assignment procedure: first, the edge with the highest score is labeled as a true edge, with the jet assigned to this parton. Next, all edges connected to the corresponding jet and parton are removed, and the next highest edge is chosen. This process continues until all six partons are assigned, ensuring each jet and each parton is used exactly once.
-
Regression for Intermediate Particle Properties: Beyond just solving the assignment problem, Topographs predict the kinematic properties (three-momentum components) of the intermediate W bosons and top quarks through dedicated regression networks. These predictions are trained using the truth-level properties of the particles, providing more accurate and less biased estimates than simply reconstructing these quantities from the assigned jets.
By incorporating these physics-inspired structures and direct predictions, Topographs not only solve the combinatorial assignment problem but also provide a more complete and accurate reconstruction of the particle physics process. The approach scales linearly with the number of reconstructed objects, making it computationally feasible even for high-multiplicity events.
Performance and Significance: Outperforming the State-of-the-Art
We applied Topographs to the challenging case of top quark pair production in the all-hadronic decay channel, training and evaluating on a dataset of 20 million simulated events. Our results demonstrate that Topographs:
-
Outperform traditional methods: Topographs significantly outperform the χ² method in event reconstruction efficiency, showing an improvement of around 10 percentage points, especially at higher jet multiplicities. For events with exactly six jets and at least two b-tagged jets, Topographs achieve 81.7% efficiency compared to 72.7% for the χ² method. This means Topographs are much better at correctly identifying which jets came from which parent particles.
-
Match state-of-the-art machine learning techniques: Topographs achieve performance comparable to SPANet, a leading machine learning technique in this field, in terms of overall reconstruction efficiency. Both methods show similar performance across all jet multiplicities, with sub-percent differences in reconstruction efficiencies, indicating that Topographs are a competitive and powerful alternative to existing advanced methods.
-
Provide richer information: Beyond just assigning jets, Topographs directly predict the kinematic properties (momentum, energy) of the intermediate W bosons and top quarks. For correctly assigned events, these predictions show improved resolution compared to those obtained by simply reconstructing these quantities from the assigned jets. The regression predictions demonstrate narrower peaks and reduced bias, providing more accurate estimates of the intermediate particle properties.
-
Scalability: The linear scaling of Topographs with the number of reconstructed objects is a major breakthrough. While our implementation includes fully connected message passing layers for information exchange (which introduces quadratic scaling), the core Topograph structure scales linearly. This means that as experiments at the LHC become even more complex, producing events with even higher particle multiplicities, the fundamental Topograph approach will remain computationally feasible, unlike traditional methods that quickly become intractable.
-
Interpretability: The individual edge scores from Topographs can be aggregated to provide a confidence measure for the combinatorial assignment. This allows for event filtering based on assignment confidence and helps identify events where complete reconstruction may not be possible due to missing partons.
Impact on Particle Physics
The development of Topographs represents a significant step forward in particle physics event reconstruction. By combining the power of graph neural networks with a deep understanding of particle physics principles, Topographs offer a robust and efficient solution to a long-standing challenge. This innovation has several key implications:
-
Enhanced Discovery Potential: More accurate and efficient event reconstruction allows physicists to better analyze complex collision events, potentially leading to the discovery of new particles or phenomena that were previously hidden in the noise.
-
Improved Precision Measurements: The ability to precisely predict the properties of intermediate particles will enable more accurate measurements of fundamental particle properties, helping to refine our understanding of the Standard Model of particle physics and search for deviations that could hint at new physics. The regression capabilities of Topographs provide less biased estimates of particle kinematics, crucial for precision measurements.
-
Future-Proofing Analyses: As the LHC undergoes upgrades and future colliders are designed to produce even more complex events, the linear scaling of Topographs ensures that event reconstruction remains a tractable problem, paving the way for future discoveries. The modular nature of Topographs also allows them to be adapted to different physics processes beyond top quark pair production.
-
Broader Applications: The Topograph approach is not limited to top quark physics. Due to their modular design based on particle blocks, Topographs can be generalized to almost any particle physics process. Applications could extend to jet identification, reconstructing displaced vertices from heavy flavor hadron decays, or analyzing constituents in large radius jets in boosted topologies.
In essence, Topographs are not just a new algorithm; they represent a new way of thinking about event reconstruction in particle physics, offering a powerful tool to unlock the universe’s deepest secrets through more accurate and efficient analysis of high-energy collision data.
Publication:
Authors: Lukas Ehrke, John Andrew Raine, Knut Zoch, Manuel Guth, and Tobias Golling.
Title: Topological Reconstruction of Particle Physics Processes using Graph Neural Networks.
Reference: Phys. Rev. D 107 (2023) 116019.
DOI:10.1103/PhysRevD.107.116019
|
arXiv:2303.13937.