In the realm of particle physics, experiments at facilities like the Large Hadron Collider (LHC) at CERN are designed to meticulously measure the products of high-energy proton-proton collisions. Detectors like ATLAS and CMS are built to capture nearly all stable particles produced, allowing physicists to reconstruct the intricate details of fundamental interactions. This process, known as event reconstruction, is crucial for uncovering new phenomena and making precise measurements of particle properties.
However, there’s a elusive particle that poses a unique challenge: the neutrino. Neutrinos are famously shy; they interact only through the weak nuclear force and typically pass through detector material without leaving any measurable signal. Their presence is inferred indirectly, by measuring the momentum imbalance of all visible particles in the plane perpendicular to the beam pipe. This imbalance is called missing transverse momentum, and it serves as our experimental proxy for the net transverse momentum of all undetected particles. Crucially, there’s no such direct measurement for the neutrino’s momentum in the longitudinal direction, leaving its full kinematics largely unknown.
Many analyses in collider physics investigate processes that involve neutrino production. A prime example is the study of the top quark, the most massive elementary particle. Top quarks decay almost instantaneously, and about a third of the time, their decay products include a W boson that subsequently decays leptonically, producing a neutrino. To fully reconstruct the top quark system and precisely measure its properties, knowing the neutrino’s full momentum is vital. Traditional methods for estimating neutrino momentum, such as those based on kinematic constraints (e.g., assuming the W boson’s mass), often have drawbacks: they can introduce biases, may not yield real solutions, or can result in ambiguous multiple solutions without a clear way to choose the correct one.
This is where ν-Flows comes in. We introduce a novel machine learning approach designed to fully reconstruct the neutrinos produced in collisions from the missing transverse momentum and observed event kinematics. Our method moves beyond single-point estimates, instead providing a probabilistic approach that can give the likelihood over a range of viable solutions, offering a more complete and accurate picture of the neutrino’s momentum.
ν-Flows: A Probabilistic Approach with Conditional Normalizing Flows
At its core, ν-Flows utilizes conditional normalizing flows, which are powerful deep invertible neural networks (INNs). Normalizing flows are essentially sophisticated mathematical functions that can map a complex probability distribution (like the unknown neutrino momentum) into a simpler, well-understood distribution (like a standard normal distribution). The ‘conditional’ aspect means that this mapping is influenced by other observed information from the event, such as the kinematics of other particles.
Unlike traditional methods that provide a single, often ambiguous, solution for the neutrino’s momentum, ν-Flows learns the full conditional likelihood over the neutrino’s kinematics. This means it can tell us not just one possible value, but the probability of a range of values, along with interpretable uncertainties. This is a significant advantage, as it allows us to recover degrees of freedom that were previously unconstrained.
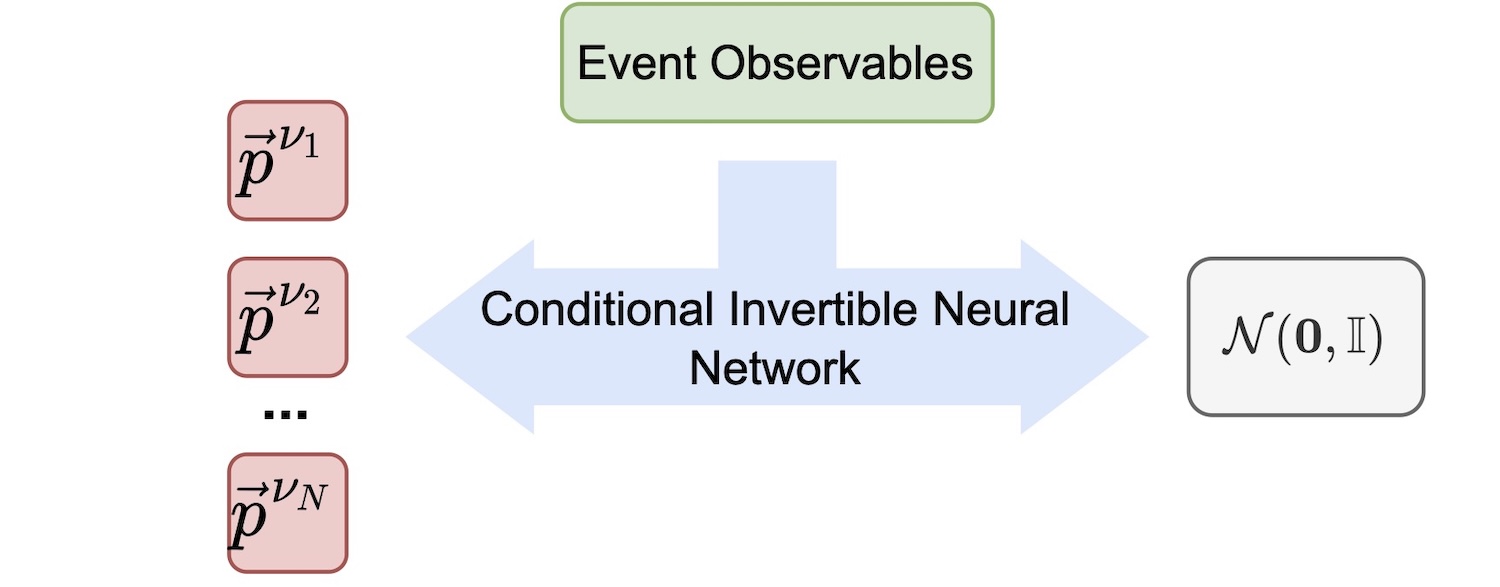Figure: A schematic overview of the conditional invertible neural network (INN) used in ν-Flows. It shows how observed event variables are used to condition the prediction of the neutrino momentum vector. (Image: SciPost Phys. 14 (2023) 159)
How ν-Flows Works
-
Learning from Data: ν-Flows is trained on simulated particle collision events where the true neutrino kinematics are known. This allows the model to learn the complex probabilistic relationship between the observed particles (leptons, jets, missing transverse momentum) and the unobserved neutrino’s momentum.
-
Conditional Inputs: The network takes various observed event variables as conditioning inputs. These include the components of the missing transverse momentum, the kinematics of the signal lepton, the kinematics and b-tagging information of the reconstructed jets, and event-level information like jet multiplicities. A Deep Set architecture is used to efficiently process the variable number of jets in an event.
-
Invertible Neural Networks: The core of ν-Flows is built using conditional invertible neural networks (INNs). These networks are designed to be bijective (meaning they have a unique inverse), efficiently invertible, and have a tractable Jacobian. This allows for efficient density estimation and the generation of new data by sampling from the learned probability distribution.
-
Probabilistic Output: Instead of a single value, ν-Flows outputs a full probability distribution for the neutrino’s momentum. This distribution can be multi-modal, reflecting the inherent ambiguities in neutrino reconstruction, such as the two solutions from the W boson mass constraint. The model learns to reproduce these physical relationships directly from the data.
-
Sampling and Mode Estimation: From the learned conditional probability density, we can either sample individual neutrino momentum values, denoted ν-Flows(sample), or identify the most probable solution, ν-Flows(mode). While sampling provides a less biased estimate, the mode estimation offers a more precise point estimate by selecting the peak of the distribution.
By leveraging these techniques, ν-Flows provides a powerful and flexible framework for neutrino reconstruction, moving beyond deterministic solutions to offer a comprehensive probabilistic understanding of the invisible particle’s kinematics.
Performance and Impact: Outperforming Traditional Methods
We demonstrated the applicability of ν-Flows in a case study involving semileptonic top-quark pair decays, where a single neutrino is present in the final state. Our results show significant improvements over traditional methods:
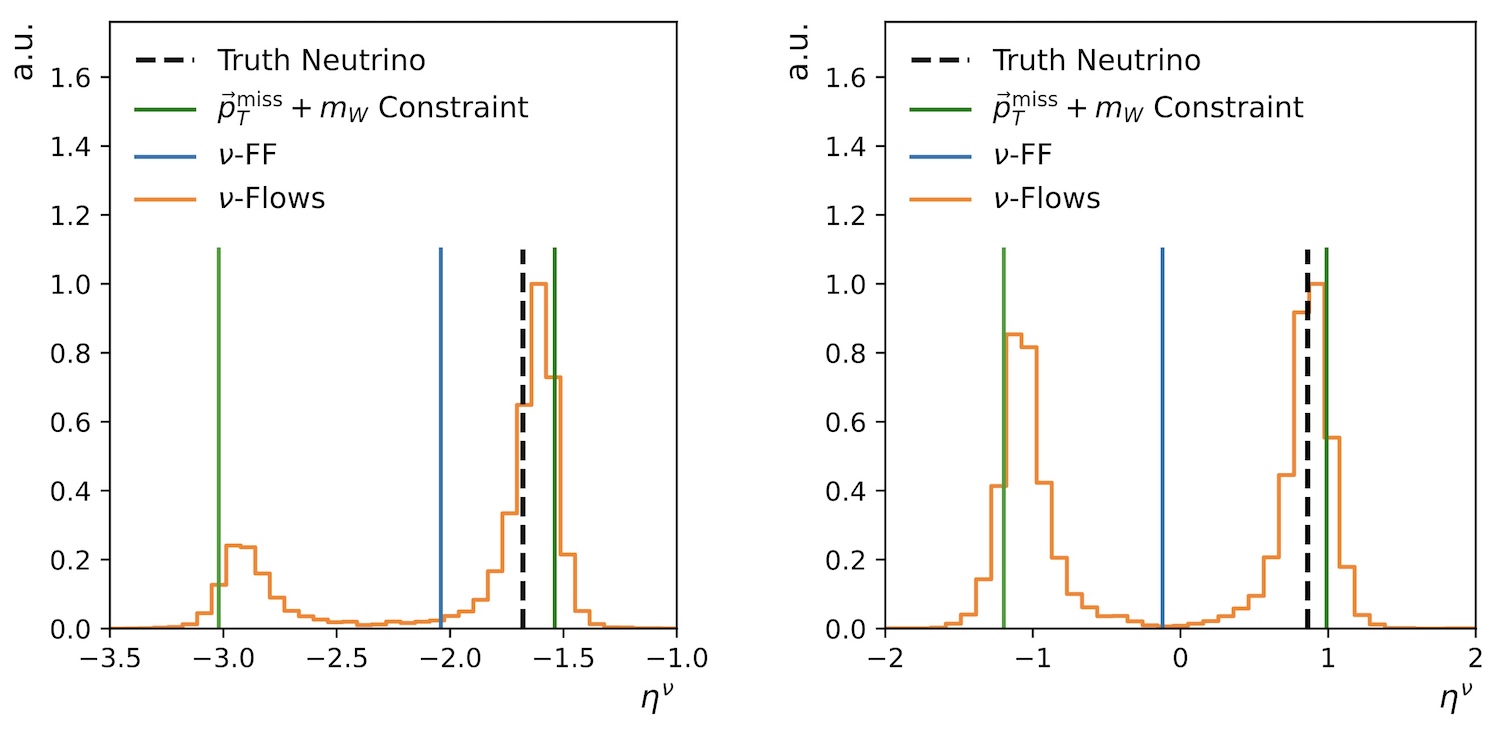Figure: Comparison of neutrino pseudorapidity (η) reconstruction for two events. The true values are shown in black. Traditional methods (green, blue) often provide ambiguous or biased point estimates, while ν-Flows (orange) provides full probability distributions, revealing the inherent uncertainties and multiple possible solutions. (Image: SciPost Phys. 14 (2023) 159)
-
Improved Momentum Reconstruction: For all components of the neutrino’s four-momentum, the distribution generated by ν-Flows(sample) closely matches the true momentum distribution. Traditional methods and even a standard feed-forward neural network (ν-FF) tend to introduce biases, particularly for the longitudinal momentum, often overestimating the fraction of events with longitudinal momentum close to zero. ν-Flows, especially in its mode estimation configuration, shows excellent correlation with the true values and no obvious bias.
-
Accurate Invariant Mass Reconstruction: ν-Flows(sample) accurately reproduces the invariant mass distribution of the lepton-neutrino system, closely matching the true distribution. While the W boson mass constraint method forces this distribution to a single value, ν-Flows learns the natural width of the W boson. For the leptonic top quark’s invariant mass, ν-Flows(mode) significantly reduces the variance and produces a distribution most similar to the true one, outperforming other methods that introduce biases or larger spreads.
-
Enhanced Jet-Parton Assignment: A crucial downstream task in many top-quark analyses is assigning reconstructed jets to their original partons. We assessed the impact of ν-Flows on this task using the χ² jet association method. Our results show that using neutrino estimates from ν-Flows (both sample and mode) leads to an improved matching efficiency compared to the standard kinematic approach. For events with nine jets, the accuracy of correctly identifying the b-jet from the leptonically decaying top quark increased by a factor of 1.41 when using ν-Flows(mode) compared to the traditional W boson mass constraint method. This improvement is particularly pronounced in events with higher jet multiplicities, where the neutrino’s kinematics play a more significant role in the assignment.
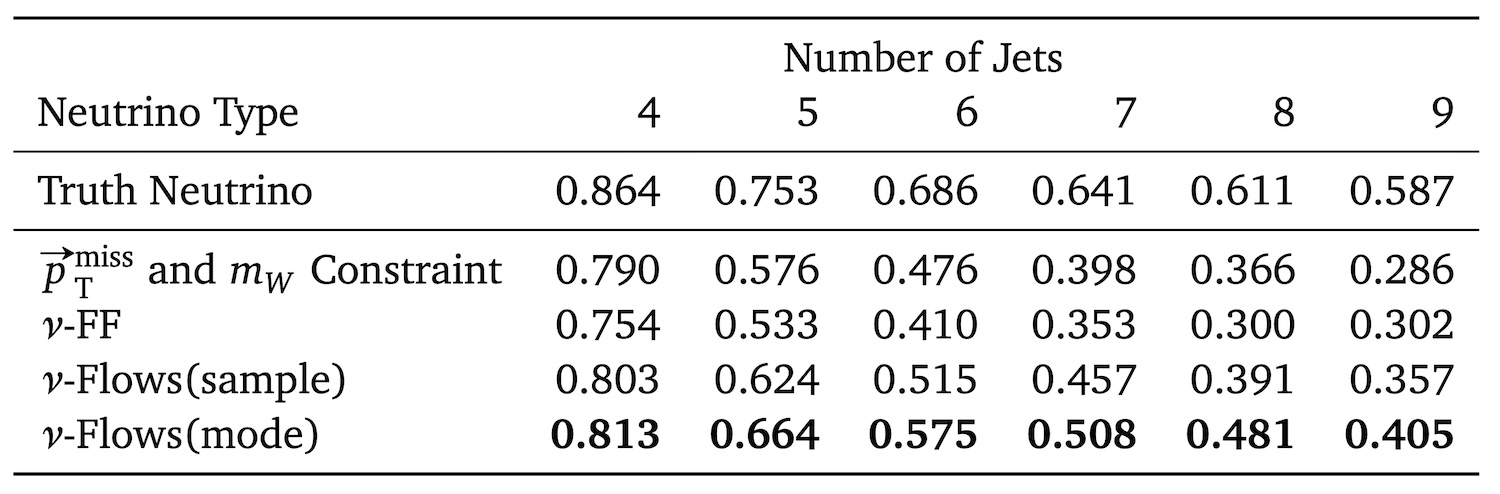Figure: The fraction of events where the correct b-jet from the leptonically decaying top quark was identified using various neutrino estimation methods, binned by the number of reconstructed jets. ν-Flows significantly improves the accuracy, especially for events with higher jet multiplicities. (Data: SciPost Phys. 14 (2023) 159)
- Interpretable Uncertainties: A key advantage of ν-Flows is its ability to provide interpretable uncertainties. For events where reconstruction is inherently difficult (e.g., due to poor detector resolution or misidentified particles), the likelihood distribution produced by ν-Flows becomes broader, indicating higher uncertainty. This allows physicists to identify and potentially filter out poorly reconstructed events from downstream analyses, leading to more robust results.
Broader Impact and Future Directions
ν-Flows represents a significant advancement in neutrino reconstruction, offering a more accurate, less biased, and probabilistically rich approach. While our initial study focused on semileptonic top-quark pair decays, the method is highly adaptable and can be extended to a wide variety of processes involving any number of invisible particles. This includes other top-quark decay channels (like dileptonic tt̄), Higgs boson studies, and even searches for physics beyond the Standard Model that predict new weakly interacting massive particles.
This work lays the groundwork for:
- Improved Precision Measurements: By providing more accurate neutrino kinematics, ν-Flows can directly enhance the precision of measurements involving neutrinos, leading to a deeper understanding of fundamental particle properties and interactions.
- Enhanced Sensitivity in Searches for New Physics: Better neutrino reconstruction means reduced uncertainties and backgrounds in searches for rare processes or new particles, potentially increasing the sensitivity of these crucial investigations.
- New Avenues for Analysis: The probabilistic nature of ν-Flows opens up new possibilities for event selection and analysis strategies, allowing physicists to leverage the full information content of neutrino kinematics.
In essence, ν-Flows provides a powerful new tool for particle physicists, enabling us to more effectively probe the universe’s deepest secrets, even those hidden by invisible particles.
Publication:
Authors: Matthew Leigh, John Andrew Raine, Knut Zoch, and Tobias Golling.
Title: ν-Flows: conditional neutrino regression.
Reference: SciPost Phys. 14 (2023) 159.
DOI:10.21468/SciPostPhys.14.6.159
|
arXiv:2207.00664.